About
I am a researcher studying how multiple fluids flow simultaneously in porous materials , such as rocks or soils. Currently, my focus is on upscaling problems in multiphase flow , using pore-scale models, thermodynamics, and statistical physics. I’m also very interested in fiber bundle models and percolation theory , where I explore the interplay between disorder, connectivity, structure and failure mechanisms. I hold a PhD in statistical physics .
Outside of research, I enjoy working withelectronics , 3D modeling, and 3D printing . By combining microcontrollers like Teensy and Arduino with additional electronics and custom 3D-printed parts, I find it fascinating how we can now build functional prototypes of various ideas right at home.
On this site, you'll find highlights of my research work, the list of my publications, and many programming tips. I will also showcase some of my electronics and 3D modeling projects. This is a new website, and I’ll be updating it regularly -stay tuned!
Outside of research, I enjoy working with
On this site, you'll find highlights of my research work, the list of my publications, and many programming tips. I will also showcase some of my electronics and 3D modeling projects. This is a new website, and I’ll be updating it regularly -
Research insights
Here are a few selected works that provide an overview of my research. Most of the related publications are open access , so feel free to explore the papers if you'd like to learn more.


When a low-viscosity fluid invades a porous medium filled with a high-viscosity fluid, viscous instabilities create finger-like displacement patterns known as viscous fingers. The growth of these fingers is generally assumed to follow linear Laplacian growth behavior. In this work, however, we show that there exists a regime where the growth can also be non-linear, following a power-law relationship with the local pressure drop.
Physics of Fluids 36, 033309 (2024)
\( S(Q_z, A_w, A_p) = -\lambda_u Q_z(\lambda_u, \lambda_w, \lambda_p) + \lambda_u Q_u + \lambda_w A_w + \lambda_p A_p\)
By defining configurational entropy for a two-component fluid system and applying Jaynes' maximum entropy principle, we derived equations analogous to classical thermodynamics for immiscible, incompressible two-phase flow in porous media. An emergent variable, agiture, is directly proportional to the pressure gradient, revealing a connection between configurational entropy and differential mobility.
Entropy 27, 121 (2025)
Publications
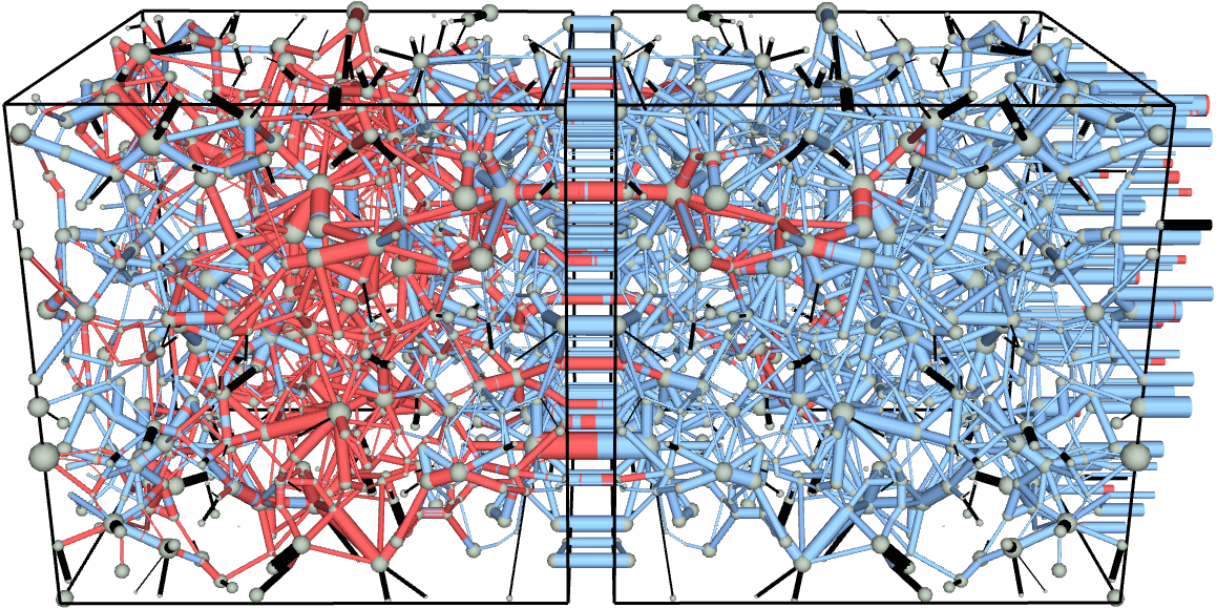
Phase transition between localized and non-localized failure during fracture growth can be first or second order depending on the type of the system disorder
Flow of two immiscible fluids in porous media at high capillary number can be described in terms of an effective viscosity with an exponent \(\alpha\) similar to an electrical network.


Full publication list
-
Thermodynamics-like Formalism for Immiscible and Incompressible Two-Phase Flow in Porous Media , A. Hansen and S. Sinha, Entropy27 , 121 (2025).
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
-
, S. Sinha, E A , .
Here is a quadratic equation: \( ax^2 + bx + c = 0 = \displaystyle\frac{1}{N}\sum_{k=1}^N \langle\sigma_i \sigma_j\rangle \)
The standard chunk of Lorem Ipsum used since the 1500s is reproduced below for those interested. Sections 1.10.32 and 1.10.33 from "de Finibus Bonorum et Malorum" by Cicero are also reproduced in their exact original form, accompanied by English versions from the 1914 translation by H. Rackham.
Contrary to popular belief, Lorem Ipsum is not simply random text. It has roots in a piece of classical Latin literature from 45 BC, making it over 2000 years old. Richard McClintock, a Latin professor at Hampden-Sydney College in Virginia, looked up one of the more obscure Latin words, consectetur, from a Lorem Ipsum passage, and going through the cites of the word in classical literature, discovered the undoubtable source. Lorem Ipsum comes from sections 1.10.32 and 1.10.33 of "de Finibus Bonorum et Malorum" (The Extremes of Good and Evil) by Cicero, written in 45 BC. This book is a treatise on the theory of ethics, very popular during the Renaissance. The first line of Lorem Ipsum, "Lorem ipsum dolor sit amet..", comes from a line in section 1.10.32.
NINE
TEN
ELEVEN
TWELVE
